해당 글은 CatlikeCoding의 튜토리얼을 실습하며 번역해놓은 글입니다. 번역 과정에서 제가 내용을 덧붙이거나 삭제한 부분이 존재합니다. 원본의 링크는 글 하단에 있습니다.
원본 글에 적혀있지 않은 내용을 추가할 때에는 (작성자 추가: ..내용)과 같은 형태로 작성하겠습니다.
요약
- 큐브 그리드를 만듭니다.
- 크기 조정, 위치 지정 및 회전을 지원합니다.
- 변환행렬로 변형을 수행합니다.
- 간단한 카메라 투영을 생성합니다.
렌더링에 기본에 대한 튜토리얼 시리즈의 첫 번째 파트입니다. 변환 행렬을 다룹니다. 렌더링 시리즈를 본격적으로 시작하기에 앞서 절차적 그리드로 시작하는 메시 기본 시리즈를 살펴봅니다. 그러면 메시가 어떻게 작동하는지 이해할 수 있습니다. 이 시리즈에서는 이러한 메시가 실제로 화면의 픽셀로 표시되는지 알아봅니다.

1. 공간 시각화
메시가 무엇이고 씬에서 메시를 어떻게 배치할 수 있는지 이미 알고 계실겁니다. 하지만 메시의 위치 지정이 실제로는 어떻게 작동하는지 알고 계신가요? 셰이더는 오브젝트를 어디에 그릴지 어떻게 알 수 있을까요? 물론 Unity의 트랜스폼 컴포넌트와 셰이더에 의존하여 모든 것을 처리할 수도 있지만, 완전한 제어를 원한다면 실제로 어떤 일이 일어나는지 이해하는 것이 중요합니다. 이 프로세스를 완전히 이해하려면 직접 구현을 해보는 것이 가장 좋습니다.
메쉬의 이동, 회전, 크기 조정은 정점의 위치를 조작하여 수행됩니다. 이는 공간의 변형이므로 실제로 작동하는 것을 보려면 공간을 시각화해야 합니다. 이를 위해 3D 포인트 그리드를 생성하겠습니다. 포인트에는 프리팹을 넣어서 사용할 수 있게 해보겠습니다.
그리드의 점을 만들기 위해 프리팹을 인스턴스화하고, 좌표를 결정하고, 색상을 지정하겠습니다. 가장 간단한 모양은 정육면체이므로 이 모양을 사용하겠습니다. 그리드의 중심은 원점이므로 변환(특히 회전 및 스케일 조정)은 그리드 큐브의 중간점을 기준으로 합니다.
using UnityEngine;
public class TransformationGrid : MonoBehaviour
{
public Transform prefab;
public int gridResolution = 10;
Transform[] grid;
void Awake ()
{
grid = new Transform[gridResolution * gridResolution * gridResolution];
for (int i = 0, z = 0; z < gridResolution; z++)
{
for (int y = 0; y < gridResolution; y++)
{
for (int x = 0; x < gridResolution; x++, i++)
{
grid[i] = CreateGridPoint(x, y, z);
}
}
}
}
Transform CreateGridPoint (int x, int y, int z)
{
Transform point = Instantiate(prefab);
point.localPosition = GetCoordinates(x, y, z);
point.GetComponent<MeshRenderer>().material.color = new Color
(
(float)x / gridResolution,
(float)y / gridResolution,
(float)z / gridResolution
);
return point;
}
Vector3 GetCoordinates (int x, int y, int z)
{
return new Vector3(
x - (gridResolution - 1) * 0.5f,
y - (gridResolution - 1) * 0.5f,
z - (gridResolution - 1) * 0.5f
);
}
}

기본 큐브를 프리팹으로 사용하고 큐브 사이에 빈 공간이 존재하도록 스케일을 절반으로 축소하겠습니다. 그리드 오브젝트를 생성하고 컴포넌트를 추가한 다음 프리팹을 연결합니다. 재생 모드로 들어가면 오브젝트의 로컬 원점을 중심으로 그리드 큐브가 나타납니다.

2. 변환(Transformations)
이상적으로, 그리드에 임의의 변환을 적용할 수 있어야 합니다. 상상할 수 있는 변형의 유형은 많지만 여기서는 이동, 회전, 크기 조정에 대해서만 알아보겠습니다. 각 변형에 대한 컴포넌트 유형을 만들면 원하는 순서와 수량으로 그리드 객체에 추가할 수 있습니다. 각 변환의 세부 사항은 다르지만 모두 공간의 한 지점에 적용할 수 있는 메서드가 필요합니다.
모든 변환 컴포넌트가 상속받을 수 있는 베이스 컴포넌트를 만들어 봅시다. 이것은 추상 클래스가 될 것이며, 이는 직접적으로 객체로 생성되어 사용할 수 없음을 의미합니다. 구체적인 변환 컴포넌트에서 작업을 수행하는데 사용할 추상 메서드 Apply()를 추가하겠습니다.
using UnityEngine;
public abstract class Transformation : MonoBehaviour
{
public abstract Vector3 Apply (Vector3 point);
}
그리드 오브젝트에 이러한 컴포넌트를 추가한 후에는 모든 그리드 포인트에 변환이 적용될 수 있도록 어떤 변환 컴포넌트가 오브젝트에 부착되어 있는지 검색할 수 있어야 합니다. 이러한 컴포넌트에 대한 참조들을 저장하기 위해 제네릭 리스트를 사용할 것입니다. 이제 변환 컴포넌트들이 담겨있는 리스트를 순회하며 그리드의 모든 점을 변환하는 기능을 'Update' 메서드에서 수행하도록 하겠습니다.
public class TransformationGrid : MonoBehaviour
{
public Transform prefab;
public int gridResolution = 10;
Transform[] grid;
List<Transformation> transformations;
void Awake ()
{
...
transformations = new List<Transformation>();
}
void Update ()
{
GetComponents<Transformation>(transformations);
for (int i = 0, z = 0; z < gridResolution; z++)
for (int y = 0; y < gridResolution; y++)
for (int x = 0; x < gridResolution; x++, i++)
grid[i].localPosition = TransformPoint(x, y, z);
}
각 점을 변형하는 작업은 원래 좌표를 가져온 다음 각 변형을 적용하는 방식으로 이루어집니다. 각 포인트의 실제 위치는 이미 변형되어 있고 매 프레임마다 변환을 누적하고 싶지 않기 때문에 각 포인트의 실제 위치에 의존할 수 없습니다.
Vector3 TransformPoint (int x, int y, int z)
{
Vector3 coordinates = GetCoordinates(x, y, z);
for (int i = 0; i < transformations.Count; i++)
coordinates = transformations[i].Apply(coordinates);
return coordinates;
}
2.1. 이동(Translation)
첫 번째로 작업할 컴포넌트는 가장 단순해 보이는 이동(Translation) 컴포넌트입니다. 'Transformation'을 확장하는 새 컴포넌트를 생성하고, 변환에 적용할 오프셋 포지션을 지정합니다. 이 컴포넌트의 Appy메서드는 원래 포인트의 포지션에 원하는 오프셋만큼 포지션값을 더해주기만 하면 됩니다.
using UnityEngine;
public class PositionTransformation : Transformation
{
public Vector3 position;
public override Vector3 Apply (Vector3 point)
{
return point + position;
}
}
이제 그리드 객체에 위치 변환 컴포넌트를 추가할 수 있습니다. 이렇게 하면 실제 그리드 객체를 움직이지 않고 모든 포인트들을 움직일 수 있습니다. 모든 변환은 오브젝트의 로컬 공간에서 이루어집니다.
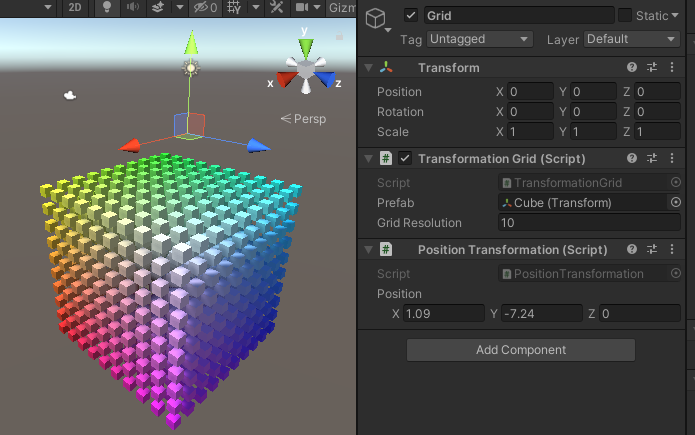
2.2. 크기 조정(Scaling)
다음은 크기 변환입니다. 배율 컴포넌트의 값을 원래 포인트에 더하는 대신 곱한다는 점을 제외하면은 이동과 거의 동일합니다.
using UnityEngine;
public class ScaleTransformation : Transformation
{
public Vector3 scale;
public override Vector3 Apply (Vector3 point)
{
point.x *= scale.x;
point.y *= scale.y;
point.z *= scale.z;
return point;
}
}
그리드 객체에도 이 컴포넌트를 추가합니다. 이제 그리드의 크기를 조정할 수 있습니다. 그리드 포인트의 위치만 조정하는 것이므로 배율을 조정해도 포인트 큐브 자체의 크기는 변경되지 않습니다.
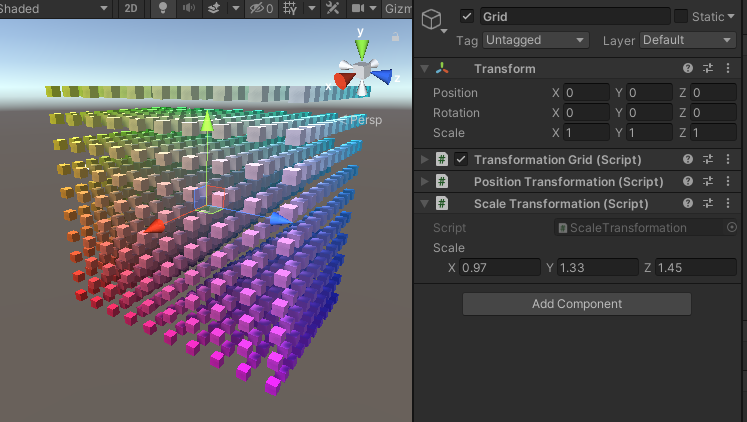
위치 지정과 크기 조정을 동시에 시도해보세요. 크기 조정이 위치에도 영향을 미친다는 것을 알 수 있습니다. 이는 먼저 공간의 위치를 변경한 다음 스케일을 조정하기 때문에 발생합니다. Unity의 트랜스폼 컴포넌트는 이 작업을 반대 방향으로 수행하므로 훨씬 더 유용합니다. 우리도 컴포넌트의 순서를 바꾸면 이 작업을 수행할 수 있습니다. 각 컴포넌트의 오른쪽 상단에 있는 톱니바퀴 아이콘 아래의 팝업 메뉴를 통해 컴포넌트를 이동할 수 있습니다.
(작성자 추가: 그냥 컴포넌트 헤더 잡고 드래그해도 이동됩니다)
2.3. 회전(Rotation)
세 번째 변형 유형으로 회전을 구현해 보겠습니다. 앞의 두가지보다 조금 더 어렵습니다. 이번 단계에서는 Z축이라는 단일 축을 중심으로 회전하는 것만 구현해보겠습니다. 이 축을 중심으로 점을 회전하는 것은 바퀴를 돌리는 것과 같습니다. Unity는 왼손 좌표계를 사용하므로 양수 방향으로 회전하면 휠이 시계 반대 방향으로 회전합니다.
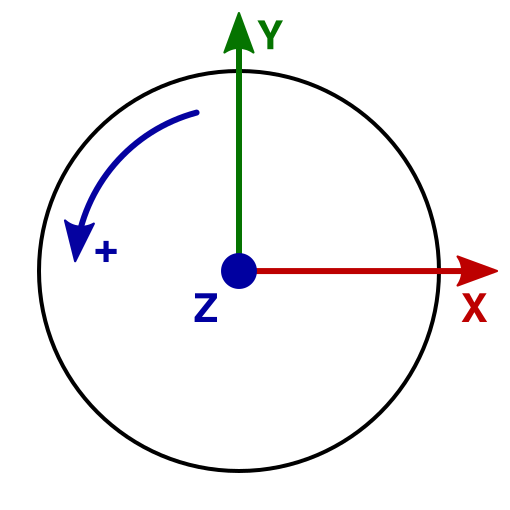
점이 회전하면 점의 좌표는 어떻게 되나요? 반지름이 1단위인 원, 즉 단위 원 위에 놓인 점을 고려하는 것이 가장 쉽습니다. 가장 간단한 점은 X축과 Y축에 해당합니다. 이러한 점을 90'씩 회전하면 항상 0, 1 또는 -1의 좌표가 됩니다.
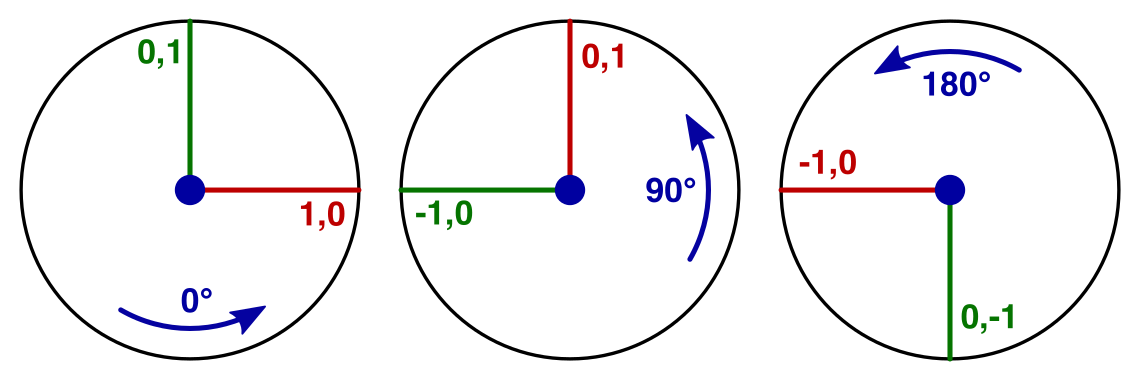
이번에는 45'단위로 회전하면 어떨까요? 그러면 XY평면의 대각선에 놓이는 점이 생성됩니다. 원점까지의 거리는 변하지 않으므로 (±√½, ±√½)의 좌표를 얻어야 합니다. 이렇게 하면 사이클이 0, √½, 1, √½, 0, -√½, -1, -√½로 확장됩니다. 스텝의 크기를 계속해서 줄이면 결국 사인파가 됩니다.
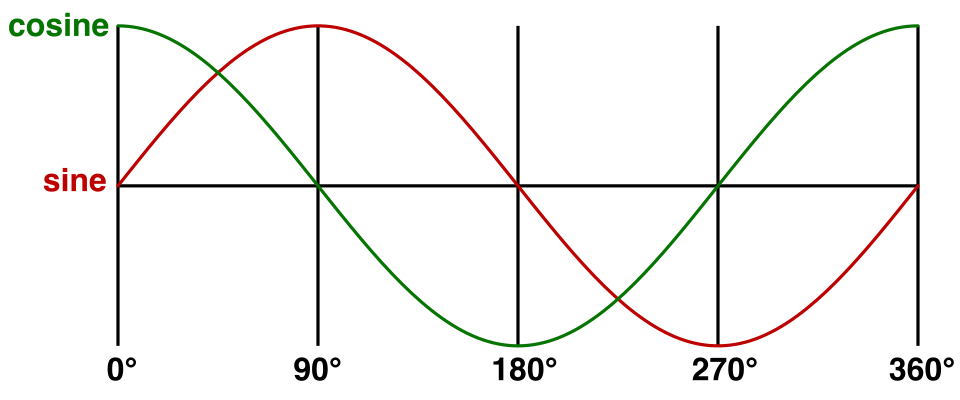
이 경우 사인파는 (1,0)에서 시작할 때 y좌표와 일치합니다. 코사인은 x좌표와 일치합니다. 즉, (1,0)을 다음과 같이 재정의 할 수 있습니다. (cos z, sin z) 마찬가지로 (0,1)을 다음과 같이 바꿀 수 있습니다.(-sin z, cos z)
따라서 Z축을 중심으로 원하는 회전의 사인과 코사인을 계산하는 것부터 시작합니다. 각도를 도 단위로 제공하지만 사인과 코사인은 라디안 단위로 작동하므로 단위를 변환해줘야 합니다.
using UnityEngine;
public class RotationTransformation : Transformation
{
public Vector3 rotation;
public override Vector3 Apply (Vector3 point)
{
float radZ = rotation.z * Mathf.Deg2Rad;
float sinZ = Mathf.Sin(radZ);
float cosZ = Mathf.Cos(radZ);
return point;
}
}
지금까지는 (1,0)과 (0,1)을 회전하였는데, 임의의 위치에 존재하는 점을 회전하는 것은 어떨까요? 우리는 모든 2d포인트 (x,y)를 xX + yY로 분해할 수 있습니다. 회전이 없는 경우 이는 다음과 같습니다. x(1,0) + y(0,1) 실제로는 그냥 (x, y)라고 할 수 있습니다. 점이 회전할 때는 x(cosZ, sinZ) + y(-sinZ, cosZ)가 회전된 지점을 가리키게 됩니다. 이를 단일 좌표 쌍으로 압축하면 다음과 같이 됩니다. (xcosZ−ysinZ,xsinZ+ycosZ).
return new Vector3(
point.x * cosZ - point.y * sinZ,
point.x * sinZ + point.y * cosZ,
point.z
);
그리드에 회전 컴포넌트를 추가하고 컴포넌트의 순서를 다음과 같이 조정합니다. 스케일 -> 회전 -> 위치. 이것이 바로 Unity의 트랜스폼 컴포넌트가 하는 일입니다. 물론 지금은 Z축을 중심으로 한 회전만 지원합니다. 다른 두 축은 나중에 다루겠습니다.
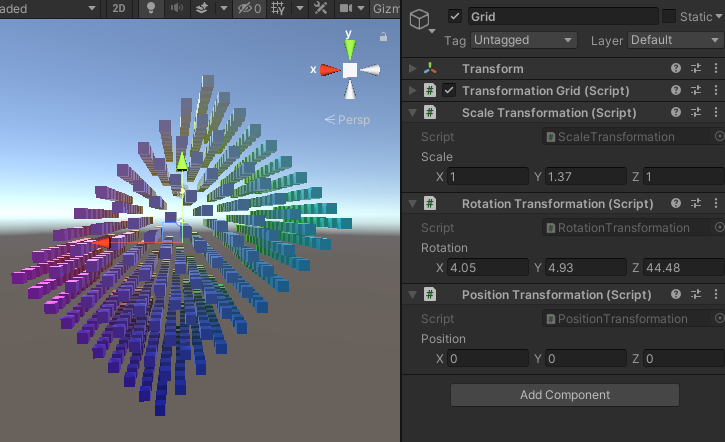
3. 모든 축의 회전
지금은 Z축을 중심으로만 회전할 수 있습니다. Unity 트랜스폼 컴포넌트와 동일한 회전 지원을 제공하려면 X축과 Y축에서도 회전을 활성화해야 합니다. 이러한 축을 개별적으로 회전하는 것은 Z축을 중심으로 회전하는 것과 비슷하지만, 여러 축을 한 번에 회전할 때는 더 복잡해집니다. 이 문제를 해결하기 위해 회전과 관련된 수학을 정리해보겠습니다.
3.1. 행렬
이제는 행렬을 사용하여 수식을 표현하겠습니다. 실제로 우리가 수행했던 곱셈은 다음과 같습니다.
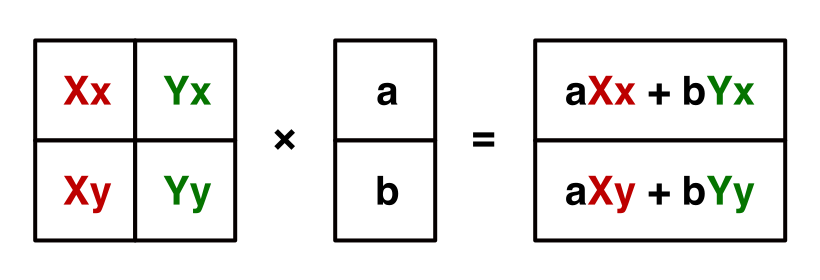
(작성자 추가: 기본적인 행렬에 대한 설명이나, 수식사용은 최소화하고 핵심 아이디어만 정리하도록 하겠습니다)
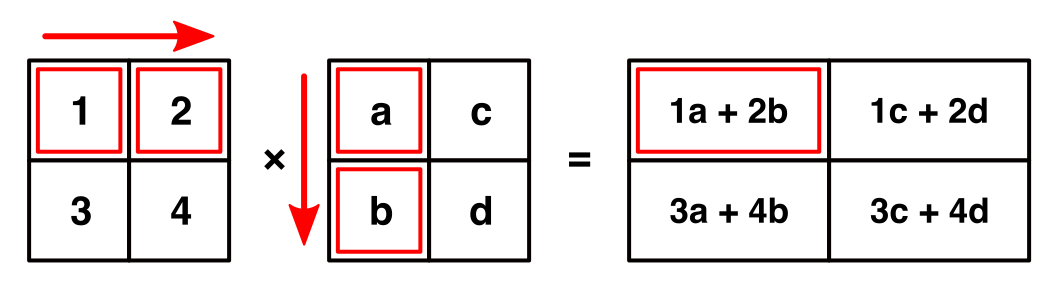
3.2. 3D 회전 행렬
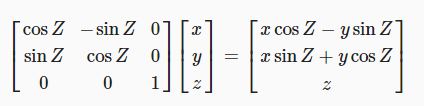
우리가 사용했던 식을 3차원 행렬로 위와 같이 표기할 수 있습니다. 우리는 2차원에 대해서만 생각했지만, 3차원에 대해 차원을 확장하려면 어떻게 해야할까요? 위와 같이 새로 추가된 차원의 대각선에 위치한 성분만 1을 대입하고, 나머지는 0을 대입하면 됩니다. 만약 대각선에 위치한 성분이 1이 아니라 0이라고 한다면, z값의 결과는 언제나 0이 되기 때문에 우리가 의도한 것이랑 다른 결과가 나오게 됩니다.
이 트릭을 모든 3차원에 사용하면 모든 대각선 성분에는 1이 있고 다른 모든 곳에는 0이 있는 행렬이 됩니다. 이를 아이덴티티 행렬이라고 하는데, 어떤 행렬에 곱해도 원래의 행렬 값이 변하지 않기 때문입니다. 모든 것을 변경하지 않고 통과시키는 필터와도 같습니다.
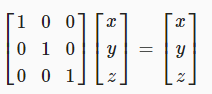
3.3. X와 Y축에 대한 회전 행렬
Z를 중심으로 회전하는 방법을 찾기 위해 적용한 것과 동일한 추론을 사용하여 Y를 중심으로 회전하는 행렬을 만들 수 있습니다.
Y축은 변경되지 않는 채로 유지되는 회전 행렬입니다.
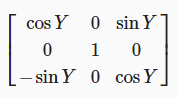
마찬가지로 X를 일정하게 유지하고 Y와 Z를 같은 방식으로 조정하는 회전 행렬입니다.
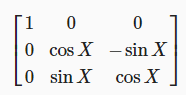
3.4. 회전 행렬의 통합
세 개의 회전 행렬은 각각 단일 축을 중심으로 회전합니다. 이들을 하나씩 결합해보겠습니다. 먼저 Z를 중심으로 회전한 다음 Y를 중심으로 회전하고 마지막으로 X를 중심으로 회전해보겠습니다. 이 회전을 변환을 적용할 포인트에 하나씩 적용 할 수도 있지만, 회전 행렬을 서로 곱해서 적용할 수 도 있습니다. 그러면 새로운 회전 행렬이 생성되어 세 가지 회전을 한 번에 적용할 수 있습니다.
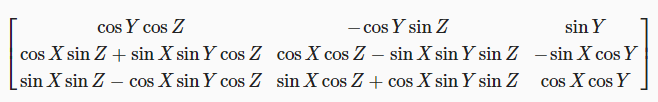
곱셈의 순서가 중요한가요?
곱셈을 어떤 순서로 계산하는지는 중요하지 않습니다. X×(Y×Z)=(X×Y)×Z. 계산 중간 단계는 다르지만 최종 결과는 모두 동일하게 나옵니다.
그러나 이 방정식에서 행렬의 순서를 바꾸면 회전 순서가 변경되어 다른 결과가 생성됩니다. X×Y×Z≠Z×Y×X. 행렬 곱셈은 이 점에서 단일 숫자를 사용한 곱셈과 다릅니다. 행렬 곱셈은 이 점에서 단일 숫자를 사용한 곱셈과 다릅니다.
유니티에서는 ZXY순서로 곱셈을 진행합니다.
이제 통합된 회전 행렬이 생겼으므로 회전 결과를 X,Y,Z축을 어떻게 구성할 수 있는지 알 수 있습니다.
public override Vector3 Apply (Vector3 point)
{
float radX = rotation.x * Mathf.Deg2Rad;
float radY = rotation.y * Mathf.Deg2Rad;
float radZ = rotation.z * Mathf.Deg2Rad;
float sinX = Mathf.Sin(radX);
float cosX = Mathf.Cos(radX);
float sinY = Mathf.Sin(radY);
float cosY = Mathf.Cos(radY);
float sinZ = Mathf.Sin(radZ);
float cosZ = Mathf.Cos(radZ);
Vector3 xAxis = new Vector3(
cosY * cosZ,
cosX * sinZ + sinX * sinY * cosZ,
sinX * sinZ - cosX * sinY * cosZ
);
Vector3 yAxis = new Vector3(
-cosY * sinZ,
cosX * cosZ - sinX * sinY * sinZ,
sinX * cosZ + cosX * sinY * sinZ
);
Vector3 zAxis = new Vector3(
sinY,
-sinX * cosY,
cosX * cosY
);
return xAxis * point.x + yAxis * point.y + zAxis * point.z;
}
4. 변환 행렬
세 가지 회전을 하나의 행렬로 통합할 수 있다면 크기 조정, 회전, 위치 변환도 하나의 행렬로 결합할 수 있을까요? 크기 조정과 위치 변경을 행렬로 표현할 수 있다면 대답은 '예' 입니다.
크기 변환 행렬은 간단하게 구성할 수 있습니다. 아이덴티티 행렬을 가지고 그 구성 요소를 스케일링 하면 됩니다.
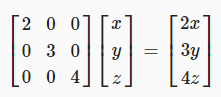
위치 이동은 어떻게 표현할 수 있을까요? 이것은 세축의 재정의가 아니라 오프셋입니다. 따라서 현재 가지고 있는 3x3 행렬로는 이를 표현할 수 없습니다. 오프셋을 포함하려면 추가 열이 필요합니다. 이를 위해서 4x4행렬과 4D포인트가 생성됩니다.
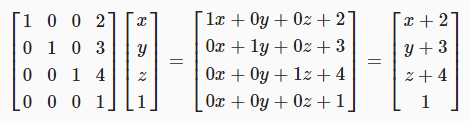
따라서 4x4 변환 행렬을 사용해야 합니다. 즉 배율 및 회전 행렬에 0이 있는 행과 열이 추가되고, 오른쪽 하단 대각성분에 1이 있습니다. 그리고 우리의 모든 포인트 항상 1인 네 번째 좌표를 얻습니다.
4.1. 동차 좌표계
네 번째 좌표가 무슨 의미인지 알 수 있을까요? 뭔가 유용한 것을 나타낼 수 있을까요? 우리는 이 좌표에 1이라는 값을 부여하여 포인트의 위치 변경을 가능하게 한다는 것을 알고 있습니다. 값이 0이면 오프셋은 무시되지만 크기 조정과 회전은 여전히 이루어집니다. 크기 조정과 회전은 가능하지만 이동은 불가능한 무언가, 이것은 점이 아니라 벡터. 즉 방향입니다. 이것은 동일한 행렬을 사용하여 위치, 법선, 탄젠트를 변환할 수 있다는 의미이므로 유용하게 사용할 수 있습니다.
그렇다면 네 번째 좌표가 0이나 1이 아닌 다른 값을 가지면 어떻게 될까요? 아무런 차이가 없어야 합니다. 우리는 이제 균등 좌표로 작업하고 있습니다. 공간의 각 점을 무한한 양의 좌표 집합으로 표현할 수 있다는 개념입니다. 가장 간단한 형태는 1을 네 번째 좌표로 사용하는 것입니다. 다른 모든 대안은 전체 집합에 임의의 숫자를 곱하면 찾을 수 있습니다.
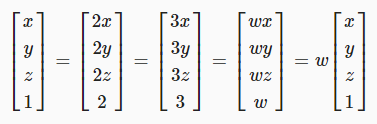
따라서 유클리드 점(실제 3d 점)을 얻으려면 각 좌표를 네 번째 좌표로 나눈 다음 버려야 합니다.
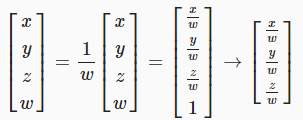
물론 네 번째 좌표가 0일 때는 작동하지 않습니다. 이러한 점은 무한히 멀리 떨어져 있는 것으로 정의됩니다. 그렇기에 방향처럼 작동합니다.
4.2. 행렬 사용하기
Unity의 Matrix4x4 구조체를 사용하여 행렬 곱셈을 수행할 수 있습니다. 이제부터는 현재 방식 대신 이 구조를 사용하여 변환을 수행하겠습니다. 먼저 추상 클래스인 Transformation을 아래와 같이 변경하겠습니다. 'Apply'메서드는 이제 더 이상 추상적일 필요가 없습니다. 행렬을 가져와 곱셈을 수행하기만 하면 됩니다.
using UnityEngine;
public abstract class Transformation : MonoBehaviour
{
public abstract Matrix4x4 Matrix { get; }
public Vector3 Apply (Vector3 point) => Matrix.MultiplyPoint(point);
}
Matrix4x4.MultiplyPoint에는 3D벡터 매개변수가 있다는 점에 유의하세요. 누락된 네 번째 좌표가 1이라고 가정됩니다. 또한 동차 좌표계에서 유클리드 좌표로 다시 변환하는 작업도 처리합니다. 점 대신 방향에 대한 곱셈을 수행하려면 Matrix4x4.MultiplyVector를 사용할 수 있습니다. 이제 구체적인 변환 클래스는 적용 메서드를 매트릭스 프로퍼티로 변경해야 합니다.
public class PositionTransformation : Transformation
{
public Vector3 position;
public override Matrix4x4 Matrix
{
get
{
Matrix4x4 matrix = new Matrix4x4();
matrix.SetRow(0, new Vector4(1f, 0f, 0f, position.x));
matrix.SetRow(1, new Vector4(0f, 1f, 0f, position.y));
matrix.SetRow(2, new Vector4(0f, 0f, 1f, position.z));
matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
return matrix;
}
}
}public class ScaleTransformation : Transformation
{
public Vector3 scale;
public override Matrix4x4 Matrix
{
get
{
Matrix4x4 matrix = new Matrix4x4();
matrix.SetRow(0, new Vector4(scale.x, 0f, 0f, 0f));
matrix.SetRow(1, new Vector4(0f, scale.y, 0f, 0f));
matrix.SetRow(2, new Vector4(0f, 0f, scale.z, 0f));
matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
return matrix;
}
}
}public class RotationTransformation : Transformation
{
public Vector3 rotation;
public override Matrix4x4 Matrix
{
get
{
float radX = rotation.x * Mathf.Deg2Rad;
float radY = rotation.y * Mathf.Deg2Rad;
float radZ = rotation.z * Mathf.Deg2Rad;
float sinX = Mathf.Sin(radX);
float cosX = Mathf.Cos(radX);
float sinY = Mathf.Sin(radY);
float cosY = Mathf.Cos(radY);
float sinZ = Mathf.Sin(radZ);
float cosZ = Mathf.Cos(radZ);
Matrix4x4 matrix = new Matrix4x4();
matrix.SetColumn(0, new Vector4(
cosY * cosZ,
cosX * sinZ + sinX * sinY * cosZ,
sinX * sinZ - cosX * sinY * cosZ,
0f
));
matrix.SetColumn(1, new Vector4(
-cosY * sinZ,
cosX * cosZ - sinX * sinY * sinZ,
sinX * cosZ + cosX * sinY * sinZ,
0f
));
matrix.SetColumn(2, new Vector4(
sinY,
-sinX * cosY,
cosX * cosY,
0f
));
matrix.SetColumn(3, new Vector4(0f, 0f, 0f, 1f));
return matrix;
}
}
}
4.3. 매트릭스 합치기
이제 변환 행렬을 단일 행렬로 결합해보겠습니다. 그리드의 변환 행렬을 업데이트 타이밍마다 업데이트 하겠습니다. 여기에는 첫 번째 행렬을 가져온 다음 다른 모든 행렬을 곱하는 작업이 포함됩니다. 이는 올바른 순서대로 곱해야 합니다.
// TransformationGrid.cs
Matrix4x4 transformation;
void Update ()
{
UpdateTransformation();
for (int i = 0, z = 0; z < gridResolution; z++)
for (int y = 0; y < gridResolution; y++)
for (int x = 0; x < gridResolution; x++, i++)
grid[i].localPosition = TransformPoint(x, y, z);
}
void UpdateTransformation ()
{
GetComponents(transformations);
if (transformations.Count > 0)
{
transformation = transformations[0].Matrix;
for (int i = 1; i < transformations.Count; i++)
transformation = transformations[i].Matrix * transformation;
}
}
이제 포인트의 변환에 'Apply'메서드를 사용하는 것이 아닌, 통합된 변환 행렬들을 포인트에 직접 곱해주도록 하겠습니다.
Vector3 TransformPoint (int x, int y, int z)
{
Vector3 coordinates = GetCoordinates(x, y, z);
return transformation.MultiplyPoint(coordinates);
}
이전에는 모든 포인트에 대해 각 변환 행렬을 개별적으로 생성하여 하나씩 적용했지만, 이 새로운 접근 방식이 더 효율적입니다. 이제 통합 트랜스폼 행렬을 한 번 사용하여 모든 포인트에 재사용합니다. 유니티는 동일한 기법을 사용하여 모든 오브젝트 계층 구조를 하나의 트랜스폼 행렬로 줄였습니다.
저희의 경우 훨씬 더 효율적으로 만들 수 있었습니다. 모든 변환 행렬의 마지막 행이 [0 0 0 1]로 동일하기 때문입니다. 이 사실을 알면 그 행을 잊어버리고 마지막 행에 대한 계산을 생략할 수 있습니다. Matrix4x4.MultiplyPoint4x3 메서드가 바로 이 작업을 수행합니다. 그러나 맨 아래 행을 변경하는 유용한 변환이 있기 때문에 이 메서드는 사용하지 않겠습니다.
(작성자 추가: 변환 컴포넌트에 순서에 대한 중요성이 계속 언급되는데, 관련해서 더 궁금하신 분들은 아래 글을 참조해보셔도 좋을 것 같습니다)
[ Direct ] 렌더링 파이프 라인
- 렌더링 파이프 라인 - 렌더링 파이...
blog.naver.com
5. 투영 행렬
지금까지는 3D의 한 위치에서 3D공간의 다른 위치로 점을 변환하는 작업을 진행해왔습니다. 하지만 이 점들이 2D 디스플레이에 어떻게 그려지고 있을까요? 이를 위해서 3D 공간에서 2D 공간으로의 변환이 필요합니다. 이를 위해 새로운 변환 행렬을 만들 수 있습니다!
이번에는 카메라 투영에 대한 새로운 변환을 만들어보겠습니다. 아이덴티티 매트릭스부터 시작하겠습니다.
using UnityEngine;
public class CameraTransformation : Transformation
{
public override Matrix4x4 Matrix
{
get {
Matrix4x4 matrix = new Matrix4x4();
matrix.SetRow(0, new Vector4(1f, 0f, 0f, 0f));
matrix.SetRow(1, new Vector4(0f, 1f, 0f, 0f));
matrix.SetRow(2, new Vector4(0f, 0f, 1f, 0f));
matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
return matrix;
}
}
}
이것을 그리드 오브젝트에 최종 변환으로 추가합니다.
5.1. 직교투영 카메라
3D에서 2D로 전환하는 가장 간단한 방법은 단순히 한 차원을 버리는 것입니다. 그러면 3D 공간이 평평한 평면으로 축소됩니다. 이 평면은 장면을 렌더링하는데 사용되는 실제 캔버스처럼 작동합니다. Z차원을 삭제하고 어떤 일이 일어나는지 살펴보겠습니다.
public override Matrix4x4 Matrix
{
get
{
Matrix4x4 matrix = new Matrix4x4();
matrix.SetRow(0, new Vector4(1f, 0f, 0f, 0f));
matrix.SetRow(1, new Vector4(0f, 1f, 0f, 0f));
matrix.SetRow(2, new Vector4(0f, 0f, 0f, 0f));
matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
return matrix;
}
}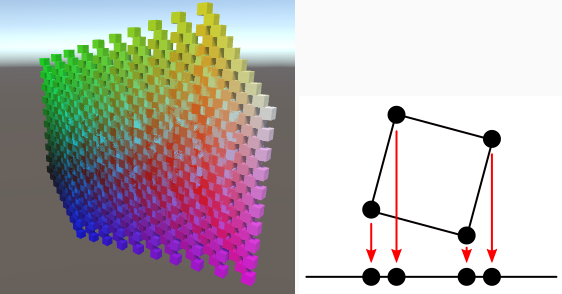
실제로 그리드는 2D가 됩니다. 여전히 모든 것을 확대, 축소, 회전, 재배치 할 수 있지만 결국 XY평면에 투영됩니다. 이것은 초보적인 직교 카메라 투영입니다.
5.2. 원근투영 카메라
직교 카메라도 좋지만 우리가 보는 세상을 그대로 보여주지 못합니다. 이를 위해서는 원근 카메라가 필요합니다. 원근법 때문에 멀리 있는 사물이 더 작게 보입니다. 카메라로부터 거리에 따라 포인트의 크기를 조정하여 이 효과를 재현할 수 있습니다.
모든 것을 Z좌표로 나누어 보겠습니다. 행렬 곱셈으로 어떻게 할 수 있을까요? 맨 아래 행을 다음과 같이 변경하면 됩니다. [0, 0, 1, 0] 그러면 네 번째 좌표가 원래의 Z좌표와 같아집니다. 그런 다음 동차 좌표에서 유클리드 좌표로 변환하면 원하는 분할이 처리됩니다.
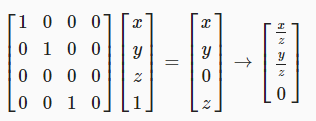
public override Matrix4x4 Matrix
{
get
{
Matrix4x4 matrix = new Matrix4x4();
matrix.SetRow(0, new Vector4(1f, 0f, 0f, 0f));
matrix.SetRow(1, new Vector4(0f, 1f, 0f, 0f));
matrix.SetRow(2, new Vector4(0f, 0f, 0f, 0f));
matrix.SetRow(3, new Vector4(0f, 0f, 1f, 0f));
return matrix;
}
}
직교 투영과 가장 큰 차이점은 점이 투영 평면에 최단거리로 이동하지 않는다는 점입니다. 대신 평면에 닿을 때까지 카메라의 위치(원점)을 향해 이동합니다. 물론 이 방법은 카메라 앞에 있는 점에만 유효합니다. 카메라 뒤에 있는 포인트는 잘못 투영됩니다. 이러한 점을 버리는 것이 아니므로 위치 변경을 통해 모든 점이 카메라 앞에 있는지 확인합니다. 그리드의 크기를 조정하거나 회전하지 않는 경우 5의 거리면 충분하지만, 그렇지 않은 경우 더 많은 거리가 필요할 수 있습니다.
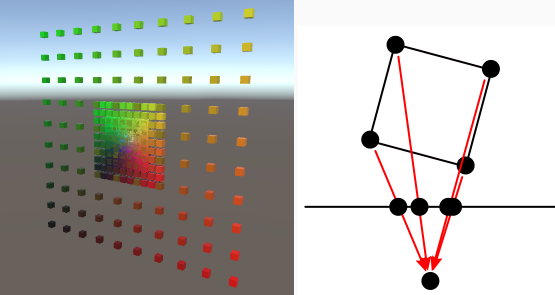
원점과 투영면 사이의 거리도 투영에 영향을 줍니다. 이는 카메라의 초점 거리와 같은 역할을 해줍니다. 초점 거리를 크게 만들수록 시야가 좁아집니다. 지금은 90' 시야를 생성하는 초점 거리 1을 사용하고 있습니다. 이를 변경 가능하게 만들 수 있습니다.
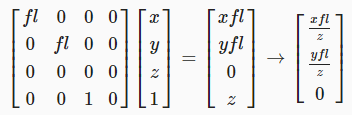
public float focalLength = 1f;
public override Matrix4x4 Matrix
{
get
{
Matrix4x4 matrix = new Matrix4x4();
matrix.SetRow(0, new Vector4(focalLength, 0f, 0f, 0f));
matrix.SetRow(1, new Vector4(0f, focalLength, 0f, 0f));
matrix.SetRow(2, new Vector4(0f, 0f, 0f, 0f));
matrix.SetRow(3, new Vector4(0f, 0f, 1f, 0f));
return matrix;
}
}
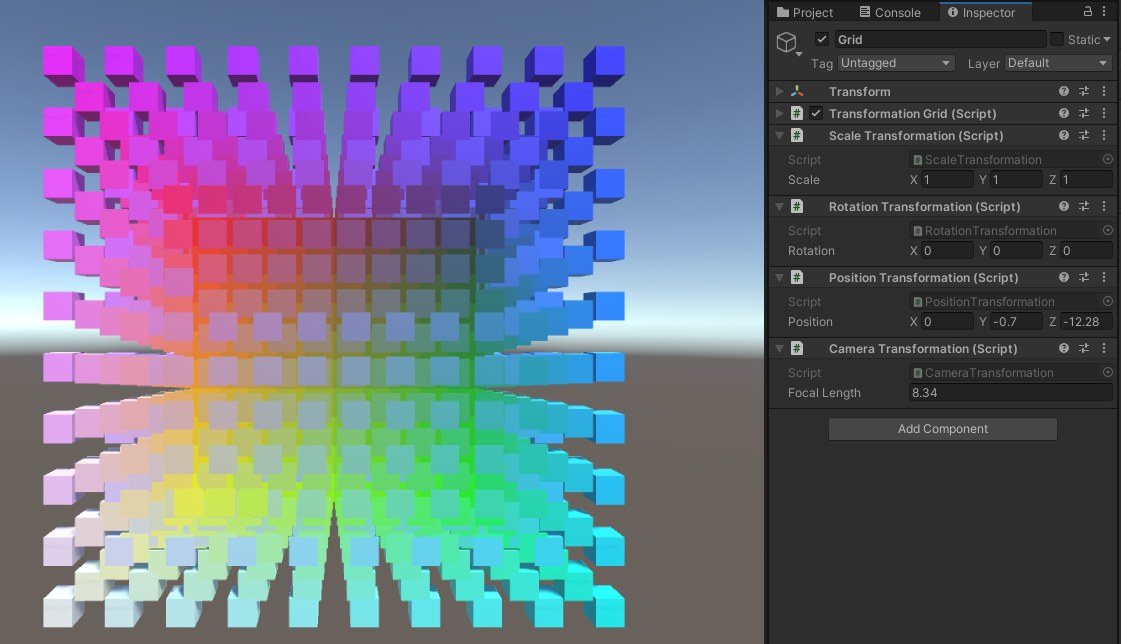
이제 아주 간단한 원근 카메라가 생겼습니다. Unity의 카메라 프로젝션을 완전히 모방하려면 근거리 및 원거리 평면도 처리해야 합니다. 그러려면 평면이 아닌 입방체에 투영해야 하므로 포인트의 깊이 정보가 유지됩니다. 그리고 뷰 종횡비도 생각해줘야 합니다. Unity의 카메라는 음의 Z방향을 바라보므로 일부 숫자를 음수화해야 합니다. 이 모든 것을 프로젝션 매트릭스에 통합할 수 있습니다. 원하신다면 직접 방법을 찾아보시길 바랍니다.
그렇다면 이번 챕터의 요점은 무엇일까요? 행렬을 직접 구성할 필요는 거의 없으며, 투영 행렬은 더더욱 아닙니다. 중요한 것은 이제 유니티 트랜스폼 내부에서 무슨 일이 일어나고 있는지 이해했다는 것입니다. 행렬은 무서운 것이 아니라 점과 벡터를 한 공간에서 다른 공간으로 변환하는 것일 뿐입니다. 어떻게 변환하는지 이해하셨죠? 셰이더를 직접 작성하기 시작하면 행렬을 다시 만나게 될 것입니다.
---
Rendering 1, Matrices, a Unity C# Tutorial
A Unity Rendering tutorial about matrices and transformations. Part 1 of 20.
catlikecoding.com
'유니티 > Catlikecoding' 카테고리의 다른 글
| [렌더링] 셰이더 기초 (Catlikecoding) (0) | 2023.08.14 |
|---|---|
| [메시 기초] 메시 변형 (Catlikecoding) (0) | 2023.08.11 |
| [메시 기초] 큐브 구체 (Catlikecoding) (0) | 2023.08.07 |
| [메시 기초] 둥근 큐브 렌더링 (Catlikecoding) (0) | 2023.08.06 |
| [메시 기초] 큐브 렌더링 (Catlikecoding) (0) | 2023.08.05 |



