해당 글은 CatlikeCoding의 튜토리얼을 실습하며 번역해놓은 글입니다. 번역 과정에서 제가 내용을 덧붙이거나 삭제한 부분이 존재합니다. 원본의 링크는 글 하단에 있습니다.
원본 글에 적혀있지 않은 내용을 추가할 때에는 (작성자 추가: ..내용)과 같은 형태로 작성하겠습니다.
요약
- 정육면체를 구체로 변환합니다.
- Unity에서 매핑을 시각화합니다.
- 변환을 비판적으로 검토합니다.
- 수학을 사용하여 더 나은 접근 방식을 생각해 보세요
1. 둥근 큐브 조정하기
지난 튜토리얼에서 둥근 큐브로 완벽한 구를 만들 수 있다는 것을 눈치 채셨을 것입니다. 큐브의 세 차원의 값을 모두 같은 값으로 변경하고 Roundness를 해당 크기의 절반으로 설정합니다.
만약 이 컴포넌트로 얻고 싶은 메시가 구라고 한다면 둥근 큐브가 제공하는 유연성은 방해만 될 뿐입니다. 따라서 이를 위한 별도의 컴포넌트를 만들어 봅시다. RoundedCube 스크립트를 복제하고 이름을 CubeSphere로 바꿉니다. 그런 다음 세 축의 크기를 하나의 gridSize로 바꾸고 Roundness 필드를 제거합니다.
public class CubeSphere : MonoBehaviour
{
public int gridSize;
private Mesh mesh;
private Vector3[] vertices;
private Vector3[] normals;
private Color32[] cubeUV;
private static int SetQuad (IList<int> triangles, int i, int v00, int v10, int v01, int v11)
{
triangles[i] = v00;
triangles[i + 1] = triangles[i + 4] = v01;
triangles[i + 2] = triangles[i + 3] = v10;
triangles[i + 5] = v11;
return i + 6;
}
private void Generate()
{
GetComponent<MeshFilter>().mesh = mesh = new Mesh();
mesh.name = "Procedural Sphere ";
CreateVertices();
CreateTriangles();
CreateColliders();
}
...
roundness필드를 제거하면 일부 사용되고 있던 위치에서 오류가 발생할 수 있습니다. 먼저 콜라이더 생성에 대해 살펴보겠습니다. 둥근 큐브를 표현하려면 여러 개의 상자 및 캡슐 콜라이더가 필요하지만 구체는 하나의 구체 콜라이더만 있으면 됩니다. 즉, AddBoxCollider와 AddCapsuleCollider 메서드를 삭제하고 CreateColliders를 한 줄의 코드로 줄일 수 있습니다.
private void CreateColliders () {
gameObject.AddComponent<SphereCollider>();
}
다음은 정점의 배치로, 이 역시 roundness에 따라 달라지고 있었습니다. 코너의 안쪽에서 원래 큐브의 어딘가를 가리키는 벡터를 정규화하여 둥근 큐브의 모서리를 형성했습니다. 구체로 바꾸면 다른 경우는 무시하고 둥글게 만들어주던 부분만 수행하면 됩니다.
구가 로컬 원점의 중앙에 있으면 편리할 것입니다. 그리드와 둥근 큐브에서는 이 작업을 수행하지 않았지만 이 경우 구의 생성이 더 간단해지므로 로컬 원점을 구의 중앙에 배치해 보겠습니다. 단위 구(반지름이 1단위인 구)를 만들려면 원점을 중심으로 하는 정육면체의 꼭지점을 정규화해야 합니다. 이 큐브가 구를 정확히 포함하려면 엣지의 길이가 2여야 합니다.
우리는 SetVertex안에서 버텍스를 만들 수 있습니다. 기존의 좌표를 grid사이즈로 나누고, 2를 곱한 다음 1을 빼주면 됩니다. 이렇게 하면 단위 구가 생성되며, radius필드를 추가하여 구의 반경을 자유롭게 변경할 수 있습니다.
public float radius = 1;
private void SetVertex (int i, int x, int y, int z) {
Vector3 v = new Vector3(x, y, z) * 2f / gridSize - Vector3.one;
normals[i] = v.normalized;
vertices[i] = normals[i] * radius;
cubeUV[i] = new Color32((byte)x, (byte)y, (byte)z, 0);
}

이제 씬에 구를 배치할 수 있습니다.
2. 매핑 조사하기

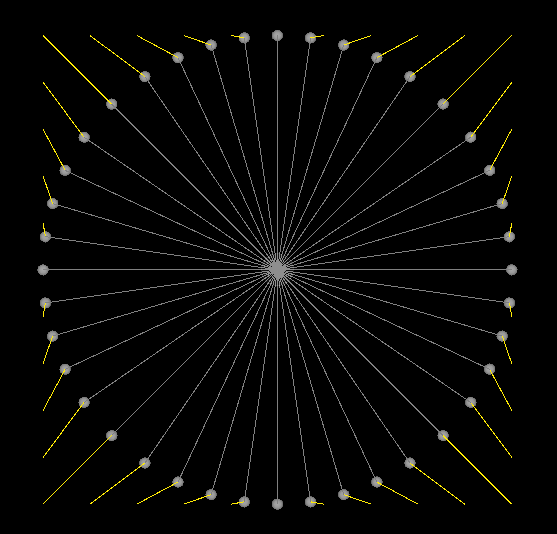
우리는 구 메시를 만들었지만, 얼마나 만족스러우신가요? 다양한 뷰에서 구를 살펴봅시다. 그리드는 얼마나 균일할까요? 그리드 셀의 크기는 상당히 다양합니다. 가장 큰 셀은 큐브 면의 중앙에서 나옵니다. 큐브 모서리에서 나오는 가장 작은 셀보다 약 4배 정도 큽니다. 그 이유를 알아보기 위해 정사각형에서 원으로의 매핑을 시각화 해보겠습니다. 원이 구보다 작업하기 쉽기 때문에 원을 사용하겠습니다. 이것은 문제의 한 부분을 쪼개서 보는 것일 뿐입니다.
Unity에서 기즈모를 사용하여 시각화를 할 수 있습니다. 여기서는 OnDrawGizmosSelected 메서드가 있는 커스텀 컴포넌트를 사용하겠습니다. 이 메서드는 OnDrawGizmos와 비슷하게 작동하지만, 오브젝트가 선택되었을때만 기즈모가 그려진다는 점이 다릅니다. 이렇게 하면 선택하지 않으면 보이지 않는 시각화 객체를 씬에 추가할 수 있습니다.
먼저 정사각형 가장자리의 곡지점을 원하는 해상도로 검은색 구체로 표시합니다. 위쪽과 아래쪽 엣지부터 시작하겠습니다.
using UnityEngine;
public class CircleGizmo : MonoBehaviour
{
public int resolution = 10;
private void OnDrawGizmosSelected ()
{
float step = 2f / resolution;
for (int i = 0; i <= resolution; i++)
{
ShowPoint(i * step - 1f, -1f);
ShowPoint(i * step - 1f, 1f);
}
}
private void ShowPoint (float x, float y)
{
Vector2 square = new Vector2(x, y);
Gizmos.color = Color.black;
Gizmos.DrawSphere(square, 0.025f);
}
}
왼쪽과 오른쪽을 채워서 사각형을 완성합니다.

private void OnDrawGizmosSelected ()
{
float step = 2f / resolution;
for (int i = 0; i <= resolution; i++)
{
ShowPoint(i * step - 1f, -1f);
ShowPoint(i * step - 1f, 1f);
}
for (int i = 1; i < resolution; i++)
{
ShowPoint(-1f, i * step - 1f);
ShowPoint(1f, i * step - 1f);
}
}
다음으로, 각 점에 대해 흰색 구를 사용하여 원의 꼭지점도 표시합니다. 그런 다음 이 두 정점 사이의 관계를 노란색 선으로 표시합니다. 마지막으로 원 꼭지점부터 중심까지 회색 선으로 표시합니다.

private void ShowPoint (float x, float y)
{
Vector2 square = new Vector2(x, y);
Vector2 circle = square.normalized;
Gizmos.color = Color.black;
Gizmos.DrawSphere(square, 0.025f);
Gizmos.color = Color.white;
Gizmos.DrawSphere(circle, 0.025f);
Gizmos.color = Color.yellow;
Gizmos.DrawLine(square, circle);
Gizmos.color = Color.gray;
Gizmos.DrawLine(circle, Vector2.zero);
}
이제 매핑이 어떻게 작동하는지 볼 수 있습니다. 정규화는 단위 원에 도달할 때까지 큐브의 정점을 중심쪽으로 끌고옵니다. 정사각형의 모서리에 가까이 있는 정점일수록 큐브의 주 축(큐브를 로컬 x축, y축)에 가까이 있는 정점보다 더 많이 당겨집니다. 실제로 주 축에 위치한 정점은 전혀 이동되지 않습니다. 반면 대각선에 정확히 위치한 정점은
vs→vc
vc=ˆvs
벡터를 정규화하려면 벡터를 자체 길이로 나누면 됩니다.
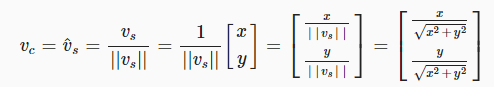
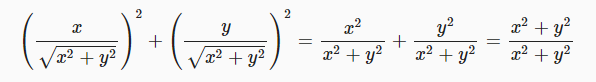
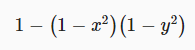
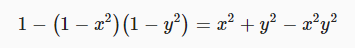
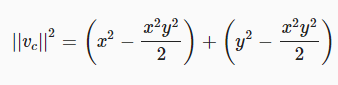
private void ShowPoint (float x, float y)
{
Vector2 square = new Vector2(x, y);
Vector2 circle;
circle.x = square.x * Mathf.Sqrt(1f - square.y * square.y * 0.5f);
circle.y = square.y * Mathf.Sqrt(1f - square.x * square.x * 0.5f);
Gizmos.color = Color.black;
Gizmos.DrawSphere(square, 0.025f);
Gizmos.color = Color.white;
Gizmos.DrawSphere(circle, 0.025f);
Gizmos.color = Color.yellow;
Gizmos.DrawLine(square, circle);
Gizmos.color = Color.gray;
Gizmos.DrawLine(circle, Vector2.zero);
}
이 매핑은 포인트를 대각선에서 축 쪽으로 밀어내는 것으로 나타났습니다. 이전 매핑과 비교해보면 인접한 점 사이의 거리가 더욱 균일해졌음을 알 수 있습니다. 개선된 것입니다.
4. 매핑 조정하기
정사각형에서 원으로 새로운 매핑을 만들었는데, 이를 큐브에서 구체로 매핑하는 것은 어떨까요? 동일한 접근방식을 사용할 수 있습니다. 기존에 있던 두 좌표에 세 번째 좌표를 통합해서 사용하면 됩니다. 이렇게 하면 단위 구의 점을 가리키는 벡터의 정사각형 길이를 얻을 수 있습니다. 실제로 이 공식은 모든 좌표계에서 작동하므로 모든 하이퍼큐브에서 같은 차원의 하이퍼 스피어까지 매핑할 수 있습니다.
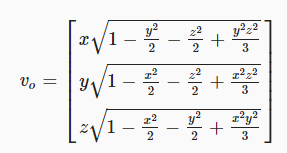

private void SetVertex (int i, int x, int y, int z)
{
Vector3 v = new Vector3(x, y, z) * 2f / gridSize - Vector3.one;
float x2 = v.x * v.x;
float y2 = v.y * v.y;
float z2 = v.z * v.z;
Vector3 s;
s.x = v.x * Mathf.Sqrt(1f - y2 / 2f - z2 / 2f + y2 * z2 / 3f);
s.y = v.y * Mathf.Sqrt(1f - x2 / 2f - z2 / 2f + x2 * z2 / 3f);
s.z = v.z * Mathf.Sqrt(1f - x2 / 2f - y2 / 2f + x2 * y2 / 3f);
normals[i] = s;
vertices[i] = normals[i] * radius;
cubeUV[i] = new Color32((byte)x, (byte)y, (byte)z, 0);
}
그리드 셀은 여전히 대각선에 가까워질수록 왜곡이 심해지는데 이를 해결할 방법이 없습니다. 하지만 이 새로운 매핑은 기존 정규화 방식보다 훨씬 더 균일한 크기의 셀을 생성합니다. 이제 축과 큐브 모서리에 있는 셀의 크기가 거의 같은 것처럼 보입니다. 처음 시작했을 때보다 훨씬 나아졌습니다! 이제 가장 큰 셀은 큐브의 엣지를 따라 있는 셀입니다. 예전에는 찌그러졌지만 이제는 늘어났습니다.
Cube Sphere, a Unity C# Tutorial
A Unity C# scripting tutorial in which we'll turn a cube into a sphere, then improve it with math.
catlikecoding.com
'유니티 > Catlikecoding' 카테고리의 다른 글
| [렌더링] 행렬 (Catlikecoding) (0) | 2023.08.12 |
|---|---|
| [메시 기초] 메시 변형 (Catlikecoding) (0) | 2023.08.11 |
| [메시 기초] 둥근 큐브 렌더링 (Catlikecoding) (0) | 2023.08.06 |
| [메시 기초] 큐브 렌더링 (Catlikecoding) (0) | 2023.08.05 |
| [메시 기초] 절차적 그리드 (Catlikecoding) (0) | 2023.08.04 |



